
Codeforces Round #739 (Div. 3)-B. Who's Opposite?
falconlee236
·2021. 12. 19. 15:33
문제 설명
짝수명의 사람이 원형으로 서있다. 각 사람의 번호는 1부터 시계방향으로 차례대로 부여한다. 각 사람은 서로 원의 중심 방향을 향해 바라보고 있으며, 반대편 사람을 지켜본다.
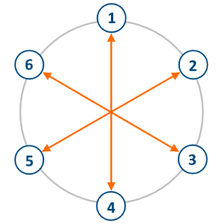
당신은 한 원에 몇명의 사람이 서있는지 모른다.(하지만 수는 반드시 짝수다.) 우리가 알고 있는 사실은 사람 $a$가 사람 $b$를 마주보고 있는 상태라는 것이다. 그렇다면 $a, b$와는 다른 수 $c$가 주어졌을 때, $c$가 마주보고 있는 사람은 어떤 수를 가지고 있는 사람일까? 만약 $a, b, c$로 원이 만들어지지 않는다면 $-1$을 출력한다.
Input
첫번째 줄에는 테스트 케이스의 수 $t (1 \le t \le 10^4)$ 이 주어진다.
각 테스트 케이스의 첫번째 줄에는 서로 다른 세 정수 $a, b, c (1 \le a, b, c \le 10^8)$ 가 주어진다.
Output
각 테스트케이스마다 이 사람들이 원형으로 서있는 상태에서 $a$번째 사람이 $b$번째 사람과 마주보고 있을 때, $c$번째 사람이 마주보는 사람의 수 $d$를 출력한다. 만약 답이 여러가지 있으면 아무거나 출력하고, 주어진 조건을 만족하는 원형 형태가 만들어 지지 않는다면 $-1$을 출력한다.
Example
input
7
6 2 4
2 3 1
2 4 10
5 3 4
1 3 2
2 5 4
4 3 2
output
8
-1
-1
-1
4
1
-1
문제 접근
사용한 알고리즘: 수학
걸린 시간 : 00:06
프로그래머가 알고리즘을 공부할 때 수학이 왜 필요한지를 깨닫게 해준 이번 문제 set중 하나이다. 나머지 하나는 다음 C번 문제이다.
일단 문제에서 강조하는 부분은 사람이 원형으로 서있다는 점이다. 만약 $a$가 $b$를 마주보고 있다면 $a$와 $b$를 잇는 선을 기준으로 양 옆에는 똑같은 사람이 서있어야 한다.
$n$명의 사람이 원형으로 서있다고 할 때, 원은 지름을 잇는 선을 기준으로 대칭이기 때문에 양 옆에는 $\frac{n - 2}{2}$ 명의 사람이 서있어야 한다.
그리고 $a$와 $b$ 사이는 $|a - b| - 1$ 명의 사람이 서있어야 한다. 왜냐하면 $1$ 부터 시계방향으로 순서대로 번호를 부여하기 때문이다. 그렇다면 이 식이 성립한다. $\frac{n - 2}{2} = |a - b| - 1$ 이 식을 $n$에 대하여 정리하면 $n = 2|a - b|$가 나온다.
그렇다면 원이 안만들어지는 경우는 어떻게 생각하면 될까? 위에서 구한 $n$보다 $a, b, c$가 크다면 말이 안되는 경우이기 때문에 $-1$을 출력한다.
$c$가 마주보고 있는 사람$d$를 구하는 방법은 위에서 구한식을 이용하면 쉽게 구할 수 있다. $\frac{n - 2}{2} = |a - b| - 1$ 이 식을 $\frac{n - 2}{2} = |c - d| - 1$ 로 바꾸면 다음 식이 나온다.
- $d = c - \frac{n}{2}$
- $d = c + \frac{n}{2}$
이 두 식에서 나온 값중에서 하나는 문제의 답이고 하나는 문제의 답이 아니다. 이것을 어떻게 판단할까?
$c \le \frac{n}{2}$ 이면 첫번째 식에 의해서 $d \le 0$ 가 된다. 사람의 번호는 1부터 시작한다고 했기 때문에 모순이다. 따라서 이 경우에는 두번째 식을 사용한다.
그렇다면 $c > \frac{n}{2}$ 일때는 첫번째 식을 사용하면 된다.
정답 코드
#include <iostream>
using namespace std;
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int t; cin >> t;
while(t--){
int a, b, c; cin >> a >> b >> c;
int n = 2 * abs(a - b);
if(a > n || b > n || c > n){
cout << -1 << "\n";
continue;
}
cout << (c > n / 2 ? c - n / 2 : c + n / 2) << "\n";
}
return 0;
}
'알고리즘 > codeforces' 카테고리의 다른 글
| Codeforces Round #739 (Div. 3)-D. Make a Power of Two (0) | 2021.12.19 |
|---|---|
| Codeforces Round #739 (Div. 3)-C. Infinity Table (0) | 2021.12.19 |
| Codeforces Round #739 (Div. 3)-A. Dislike of Threes (0) | 2021.12.19 |
| Codeforces Round #741 (Div. 2)-C. Rings (0) | 2021.12.19 |
| Codeforces Round #741 (Div. 2)-B. Scenes From a Memory (0) | 2021.12.19 |





