
Codeforces Round #747 (Div. 2)-E1. Rubik's Cube Coloring (easy version)
falconlee236
·2021. 11. 13. 19:08
문제 설명
지우는 지금 너무 배고프다. 그래서 가장 좋아하는 음식을 먹고 싶은데 일단 이 과제만 풀고 먹으려고 다짐한다. 지우가 밥을 먹을 수 있게 이 문제를 푸는 것을 도와줄 수 있을까?
자료구조에는 $2^k - 1$개 노드을 가지는 완전 이진트리를 알고 있다. 완전 이진트리는 $1$ 부터 $2^{k - 1} - 1$개 노드를 가지고 있고, 부모노드가 $i$일때 반드시 2개의 자식 노드$2i, 2i + 1$를 가지는 이진트리를 말한다. 그리고 $2{k-1}$부터 $2^k - 1$까지 번호를 가지고 있는 노드는 이 노드에서 나오는 간선이 없다는 것도 완전 이진트리의 특징이다. 우리는 이 완전 이진트리의 노드를 큐브의 6가지 색깔로 칠하고 싶다.
모든 연결된 노드가 반드시 큐브의 이웃한 색깔로 칠해지는 경우 우리는 good coloring이라고 말한다.
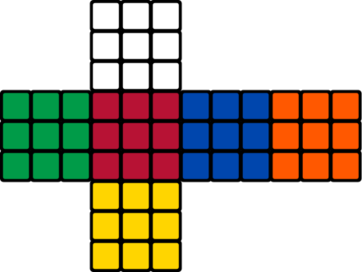
더 정확히 말하자면 다음 6개의 조건을 만족하면서 노드를 색칠해야 한다.
- 흰색 노드는 반드시 흰색 노드와 노란색 노드와 이웃해서는 안된다.
- 노란색 노드는 반드시 노란색 노드와 흰색 노드와 이웃해서는 안된다.
- 초록색 노드는 반드시 초록색 노드와 파란색 노드와 이웃해서는 안된다.
- 파란색 노드는 반드시 파란색 노드와 초록색 노드와 이웃해서는 안된다.
- 빨간색 노드는 반드시 빨간색 노드와 주황색 노드와 이웃해서는 안된다.
- 주황색 노드는 반드시 주황색노드와 빨간색 노드와 이웃해서는 안된다.
우리는 이진트리의 노드를 good coloring으로 칠할 수 있는 경우의 수를 구하고 싶다. 두 색칠은 최소 하나의 노드가 색깔이 다르면 다른 색칠으로 간주한다.
정답이 매우 크기 때문에 답을 $10^9 + 7$로 나눈 나머지 값을 출력한다.
Input
첫번째 줄에는 우리가 good coloring으로 색칠해야할 완전 이진트리의 깊이 $k$가 주어진다 $(1 \le k \le 60)$
Output
경우의 수를 $10^9 + 7$ 으로 나눈 나머지 값을 출력한다.
Example
input
3
output
24576
input
14
output
934234
문제 접근
사용한 알고리즘: 수학, 분할정복, 빠른 거듭제곱 알고리즘, 조합론
걸린 시간 : 00:12
이거 부터 풀걸 그랬다. 제발 그냥 난이도를 쉬운것 부터 차례대로 배치해줬으면 좋겠다. 경우의 수라고 쫄았더니 그냥 매우 쉬운 경우의 수 구하기였다. 이 문제를 C번보다 먼저 봤다면 한문제를 더 풀어서 1200대 퍼포먼스가 나왔을 것 같다. 가상 대회 참여를 개을리해서는 안될것 같다.
경우의 수를 구하는것은 쉽다. 첫 ROOT 노드에 색칠 할 수 있는 색깔의 경우의 수는 6이고, 루트의 자식노드들은 각각 4가지 색깔로 색칠 할 수 있다. 깊이가 $k$일 때, root노드를 제외한 노드들의 수는 $2^k - 1 - 1$이다. root를 제외한 노드들은 각각 4가지 색깔로 색칠 할 수 있기 때문에 우리가 구해야 하는 경우의 수는 $6\cdot4^{(2^k - 2)}$ 이다.
그런데 여기서 다른 문제가 발생한다. $k$의 최대값은 60인데, $2^60$ 은 long long 자료형의 최대값과 비슷한 값인데, 4를 그만큼 제곱하면 제한시간인 2초안에 절대 할 수 없다. 따라서 여기에서 분할정복의 아이디어를 이용한 빠른 거듭제곱 알고리즘을 사용한다. 이 알고리즘의 알고리즘은 $O(log(n))$ 이기 때문에 시간안에 풀 수 있다. 이 알고리즘을 잘 모르는 사람은 구글에 검색해 보자. 그러면 쉽게 구현할 수 있고, 심지어 암기할 수도 있다.
정답 코드
#include <iostream>
using namespace std;
const int mod = 1e9 + 7;
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int k; cin >> k;
long long p = (1LL << k) - 2;
long long ans = 1, tmp = 4;
while(p > 0){
if(p & 1) ans = (ans * tmp) % mod;
tmp = (tmp * tmp) % mod;
p >>= 1;
}
cout << (ans * 6LL) % mod;
return 0;
}'알고리즘 > codeforces' 카테고리의 다른 글
| Educational Codeforces Round 115 (Rated for Div. 2)-B. Groups (0) | 2021.11.16 |
|---|---|
| Educational Codeforces Round 115 (Rated for Div. 2)-A. Computer Game (0) | 2021.11.15 |
| Codeforces Round #747 (Div. 2)-C. Make Them Equal (0) | 2021.11.13 |
| Codeforces Round #747 (Div. 2)-B. Special Numbers (0) | 2021.11.13 |
| Codeforces Round #747 (Div. 2)-A. Consecutive Sum Riddle (0) | 2021.11.11 |





