
Educational Codeforces Round 112-B. Two Tables
falconlee236
·2021. 12. 25. 14:45
문제 설명
축과 평행하고 너비가 $W$이고, 높이가 $H$인 직사각형 방이 있다. 따라서 왼쪽 아래에 꼭짓점은 $(0, 0$ 이고, 오른쪽 위에 꼭짓점은 $(W, H)$ 이다.
이 방안에는 직사각형 탁자가 놓여있다. 탁자의 옆면은 벽과 평행하며, 왼쪽 아래 꼭짓점은 $(x_1, y_1)$, 오른쪽 위에 꼭짓점은 $(x_2, y_2)$ 이다.
우리는 이 방안에 너비가 $w$이고, 높이가 $h$인 또 다른 탁자를 기존의 탁자와 평행하고, 벽과 평행하게 놓고 싶다.
여기서 주의해야할 점은 두 테이블이 겹치게 놓으면 안된다는 것이다.
어떤 탁자라도 움직일 수는 없지만 첫번째 탁자를 이동시킬 수는 있다.
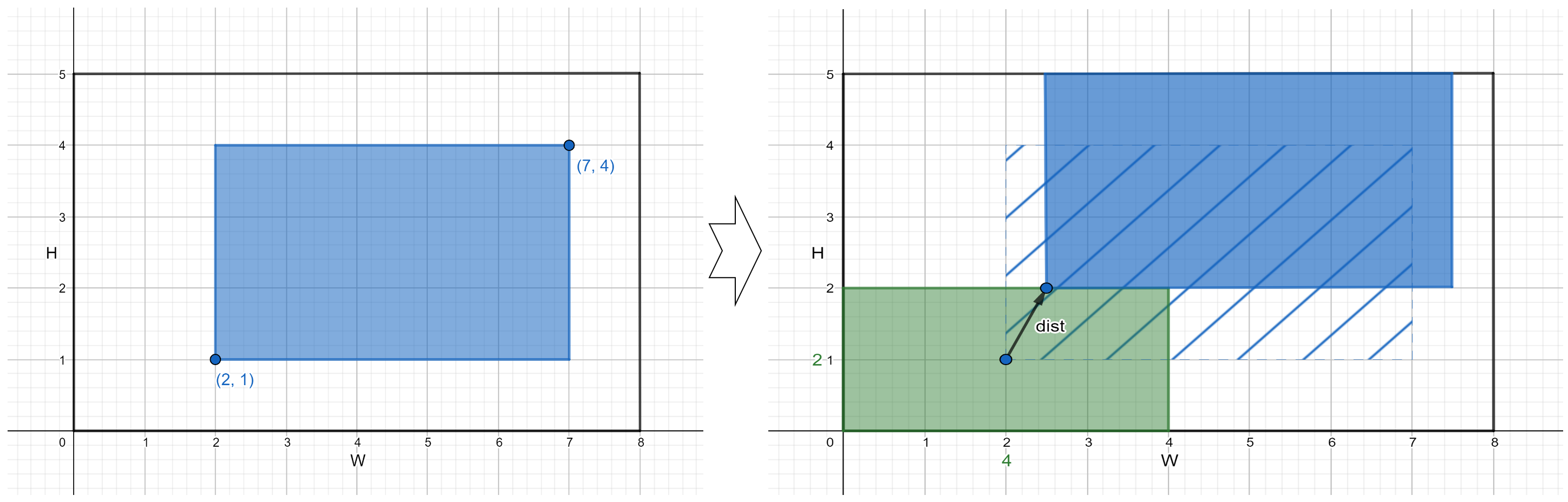
두번째 탁자가 주어진 방에 놓일 수 있게 하기 위해서 첫번째 탁자가 움직여야할 최소 거리는 무엇인가?
Input
첫번째 줄에는 테스트 케이스를 의미하는 정수 $t (1 \le t \le 5000)$ 이 주어진다.
각 테스트 케이스의 첫번째 줄에는 방의 너비와 높이를 나타내는 두 정수 $W, H (1 \le W, H \le 10^8)$ 가 주어진다.
각 테스트 케이스의 두번째 줄에는 첫번째 탁자의 꼭짓점 좌표 값인 $x_1, y_1, x_2, y_2 (0 \le x_1 < x_2 \le W, 0 \le y_1 < y_2 \le H$
각 테스트 케이스의 세번째 줄에는 두번째 탁자의 너비와 높이를 나타내는 $w, h(1 \le w \le, 1 \le h \le H)$ 가 주어진다.
Output
각 테스트케이스마다 첫번째 탁자가 움직여야할 최소 거리를 출력한다. 혹은 두번째 테이블이 들어갈 여유 공간이 없다면 $-1$을 출력한다.
Example
input
5
8 5
2 1 7 4
4 2
5 4
2 2 5 4
3 3
1 8
0 3 1 6
1 5
8 1
3 0 6 1
5 1
8 10
4 5 7 8
8 5
output
1.000000000
-1
2.000000000
2.000000000
0.000000000
문제 접근
사용한 알고리즘: 수학
걸린 시간 : 00:07
나는 수학을 정말 못하는 것 같다. 생각하는 것을 싫어하는 사람한테 PS는 지옥이다...
먼저 알아둬야 할 것은 일단 첫번째 탁자를 대각선으로 움직일 필요가 없다는 것이다. 대각선으로 움직이는 것보다 축에 평행하게 움직이는 것이 최소 거리로 움직일 수 있다. 이 점은 직접 몇번 해보면 알 수 있다. 문제에서는 소수로 출력하라고 해서 무조건 대각선으로 출력해야하는 것 같다고 생각했는데 아니였다. 진짜 문제에서 함정을 파두면 어쩌자는 건지 모르겠다.
그리고 두번째로 알 수 있는 점은 첫번째 탁자와 두번째 탁자의 너비, 높이의 합이 방의 크기를 초과하면 어떠한 방법을 써서라도 두번째 탁자를 넣을 수 없다. 너비, 혹은 높이의 합 둘중의 하나라도 값이 방의 크기보다 작다면 넣을 수 있는 방법이 있는데, 둘다 커버리면 답이 없다.
이제 문제는 첫번째 탁자를 기준으로 상하좌우에 두번째 탁자를 넣어보면서 최소 이동거리를 구하면 된다. 상하에 탁자를 넣기 위해서는 첫번째 탁자의 높이와 두번째 탁자의 높이가 방의 높이보다 작거나 같아야 한다. 아래쪽에 탁자를 넣기 위해서 움직여야할 최소 거리는 두번째 탁자높이 h에서 남아있는 공간인 $y_1$을 뺀 값만큼 움직이면 된다. 위쪽에 탁자를 넣기 위해서 움직여야할 최소 거리는 두번재 탁자 높이 h에서 남아있는 공간인 $H - y_2$를 뺀 값 만큼 움직이면 된다. 좌우도 같은 방식으로 구하면 된다.
만약 최솟값이 음수가 나왔다면 움직일 필요가 없이 널널한 경우가 있다는 뜻이므로 0을 출력한다.
정답 코드
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int t; cin >> t;
while(t--){
int W, H, x1, x2, y1, y2, w, h;
cin >> W >> H >> x1 >> y1 >> x2 >> y2 >> w >> h;
if(w + x2 - x1 > W && h + y2 - y1 > H){
cout << -1 << "\n";
continue;
}
int ans = 1e9;
if(w + x2 - x1 <= W) ans = min(ans, min(w - x1, w - (W - x2)));
if(h + y2 - y1 <= H) ans = min(ans, min(h - y1, h - (H - y2)));
if(ans < 0) ans = 0;
cout << ans << "\n";
}
return 0;
}'알고리즘 > codeforces' 카테고리의 다른 글
| Codeforces Round #737 (Div. 2) A부터 C까지 업솔빙 (0) | 2021.12.30 |
|---|---|
| Educational Codeforces Round 112-C. Coin Rows (0) | 2021.12.25 |
| Educational Codeforces Round 112-A. PizzaForces (0) | 2021.12.25 |
| Codeforces Round #736 (Div. 2)-C. Web of Lies (0) | 2021.12.20 |
| Codeforces Round #736 (Div. 2)-B. Gregor and the Pawn Game (0) | 2021.12.20 |





